BCITO Buildability

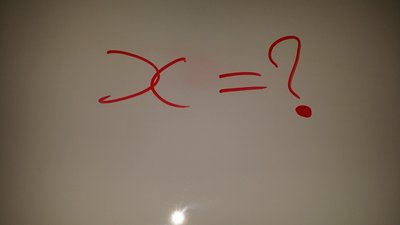
So the team having 3 students that do ncea level 3 calculus and physics have done some calculations to ensure the safety of the kids when playing on the sandpit. These calculations check that the beams of treated timber will not bend or bow too much when it is under a heavy load. using the structural rigidity of the timber and where the load of based on the beam. the team have selected to put the weight or down force in the middle of the timber so that the timber is at its maximum stress so get the maximum bend in the wood. these calculations are important if you are making a structure that floats on wheels like our sandpit does. so it is important to calculate the rotational torque around the front of the car. as well as in the middle where the main beams are connected to the front.

Consider the situation below:

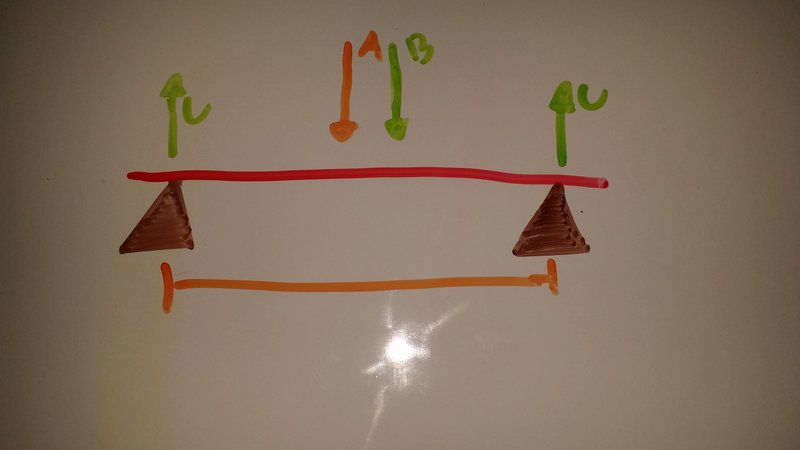
A – at this point we would put on the maximum load so that the beam starts to sag

B – this is where the weight of the beam would act

C – this is where the beam is supported which causes the sagging effect.

So if we load this beam with a large load say 200kg the there would be a deflection angle from the resting position of the beam to the where it has sagged this angle is theta. using the this angle we can calculate the sag and other relevant things such as EI.

Using the formula below:

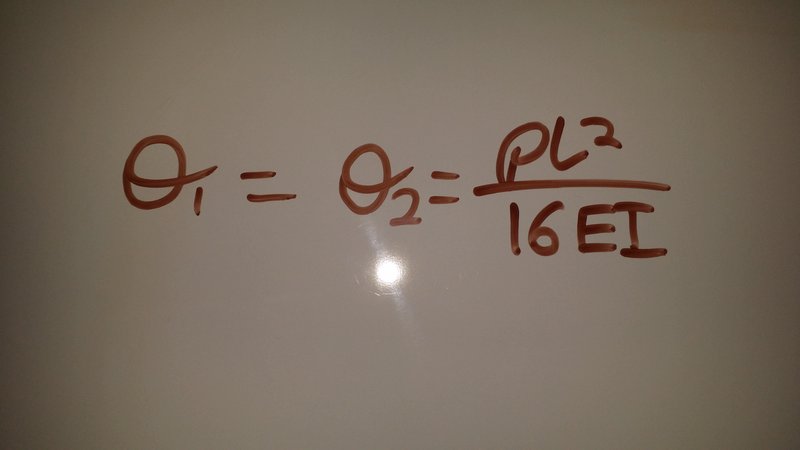
We can calculate the structural rigidity of the beam provided that we have the point load and the angle as well as the length of the beam luckily we have all three of these.

So the equation looks like this.

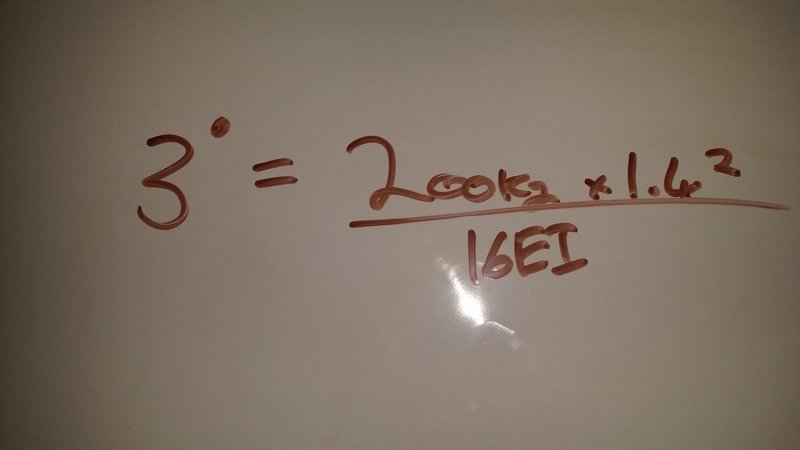
Now that we have the EI value of the beam that we have we can actually get to the fun part which is figuring out the sag of the beam using the equation below.

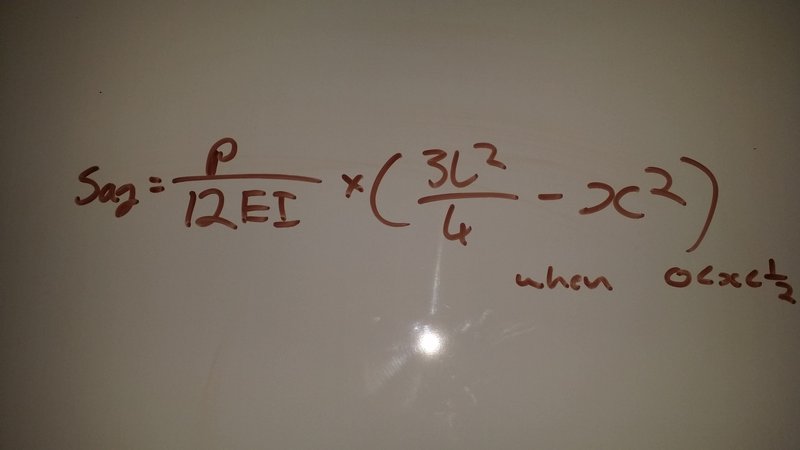
Substituting in all our values we have makes it look something like this.

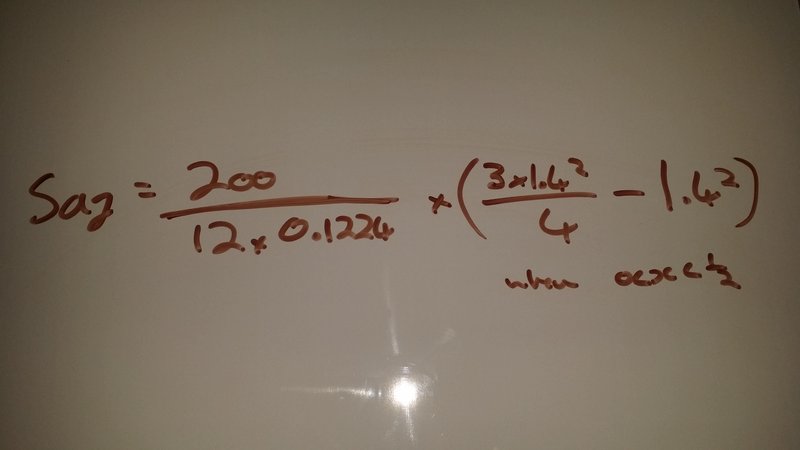
This equation tells that the beam will sag 8mm for 200kgs of weight when added in the middle of the beam. Since the team is spreading the load over 4 beams there should be minimal sag. The team have also used the regular equations such as b x h x length to work out the the total mass of the sandpit. The team believe that this will not be a problem. The problem will be the rotational torques and beam loads.